太田「まずはこちらをご覧ください。中学入試では実際にどのような問題が出されるのか見てください。」

企画戦略部 部長 太田 真光さん ：広報担当 松田 麗香さん

松田「冒頭は問題から始まるんですね。正方形の面積ですから、なんだか解けそうな気がします。」

太田「パッと見では、そんな感じがしますよね。でもこの問題、過年度、昭和薬科中学に合格した生徒の正答率は、７パーセントなんです。」

松田「じゃあ、すごく難しい問題ってことなんですね。」

太田「そうですね。今回は少し突っ込んで、難しめの問題に触れてみましょう。」

松田「今回のテーマは何でしょうか。」

太田「まず、皆さんの当面の目標は志望校合格です。ですが、そこが着地点ではなく、実はそこがスタートラインです。ガゼットに通われる生徒の皆さんが目指す学校は難関大学への進学を主眼としています。ですから、難しい問題にも果敢に挑戦するチャレンジ精神を持って勉強してほしい、ということを念頭にお話しいたします。」

松田「では、問題の解説をお願いします。」

太田「説明しやすくするために各頂点に記号をつけます。まずは頂点HとD、そして頂点BとFに補助線を引いてください。その次に頂点HとB、頂点BとD、頂点DとF、頂点FとHを結びます。何か見えてきませんか？」

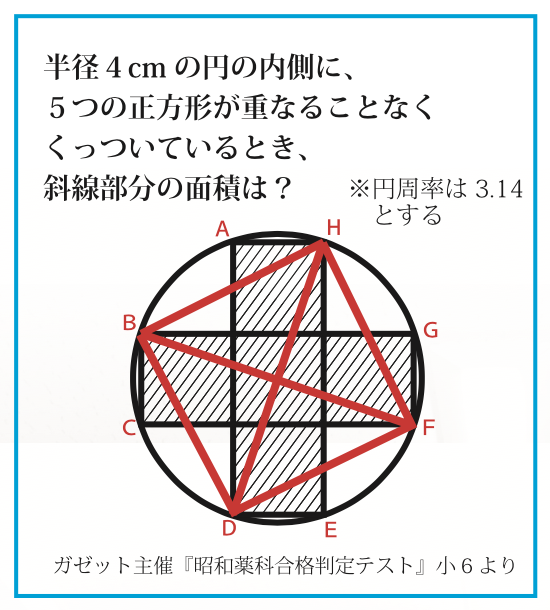
松田「円の中に正方形ができましたね。でも斜線部の面積ですか・・・等積移動ですか？」

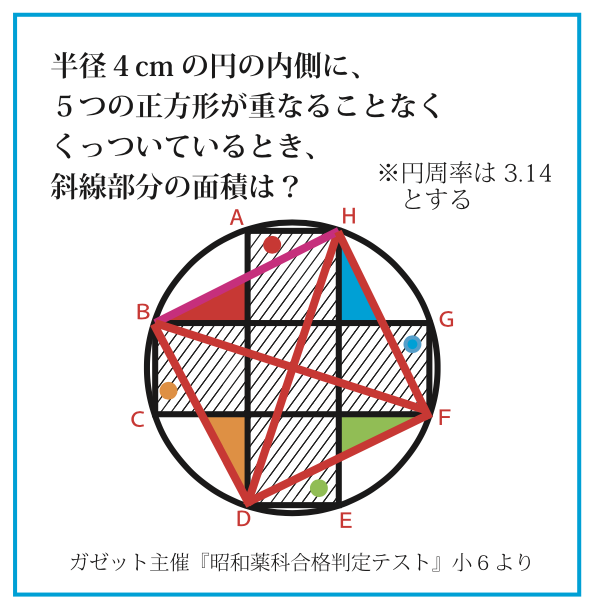
太田「当たりです。等積移動の考え方を利用します。画面内の丸印を付けた三角形を見てください。それぞれの色で結んだ三角形が合同となります。それから、もとあった斜線部の三角形4カ所を移動させてやると、正方形BDFHの中に収めることができます。」

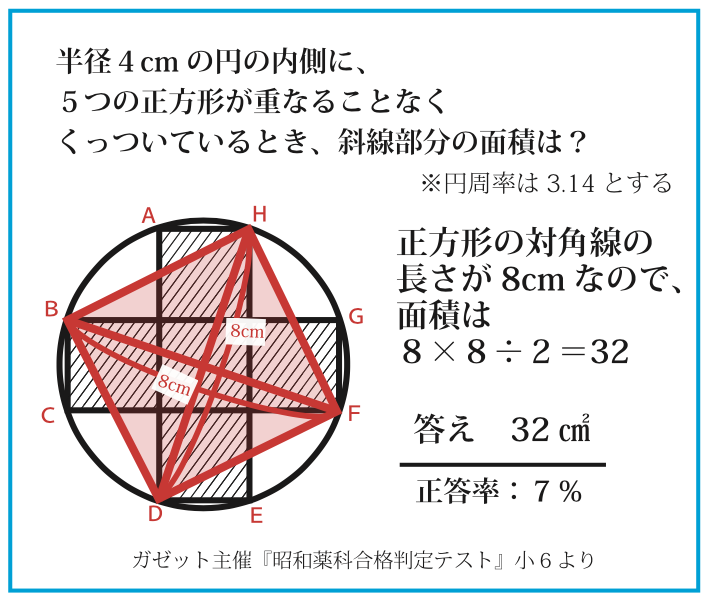
太田「正方形の面積は『一辺×一辺』のほかに『対角線×対角線÷２』でも求めることができます。正方形は半径4cmの円の中に納まっていますから、正方形の対角線の長さは、円の直径でもある８ｃｍです。そうすると正方形の面積は８×８÷２で32平方センチメートルとなります。」

太田「計算自体は非常にシンプルですが、その式にたどり着くまでが難しい問題です。」 松田「図形の問題を解く上で必要なことは、補助線を引いたり、数値を記入したり、図形をいろいろな方向から見て、図形の中に隠されたいろいろな要素を見つけることでしたね。」 太田「そのとおりです。平面図形の問題は昭和薬科中学をはじめとして、県内各私立中学および開邦中学や球陽中学の算数独自検査でも、毎年必ず出題されます。たとえばここ数年の昭和薬科中学の算数では、平面図形・立体図形の問題が全体のおよそ４分の１を占めています。」

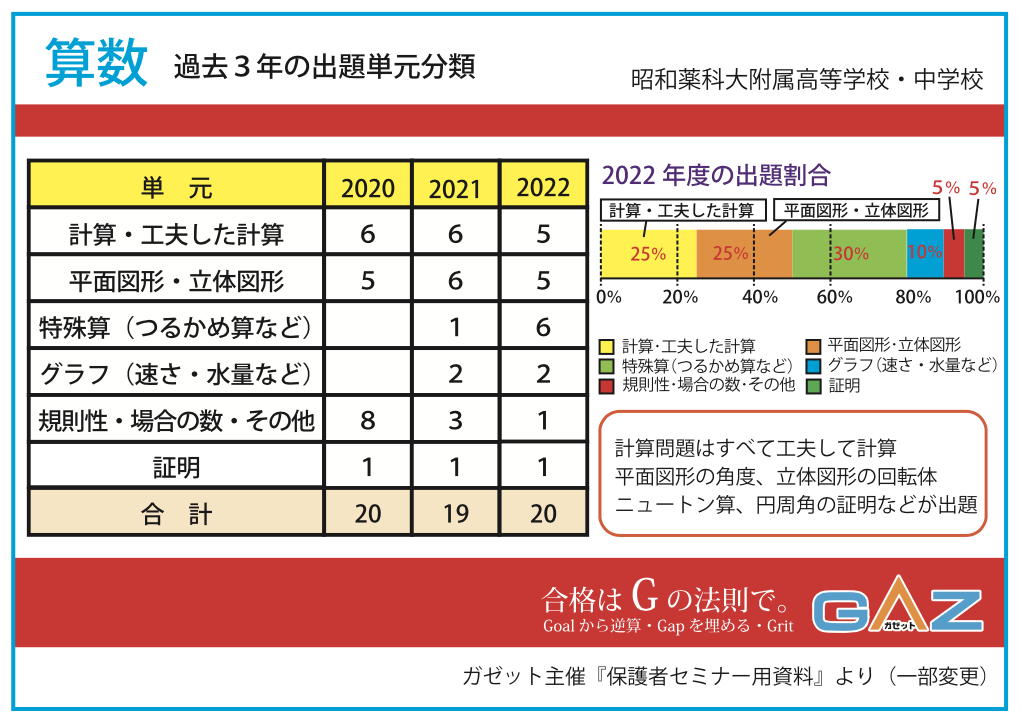
太田「その他、計算問題は必ず出題されますから、計算力に加えて、適切に処理できる『処理力』を養う必要があります。このようなデータ資料を保護者セミナーや個人面談など、ガゼットにお通いの皆様に定期的に提供いたします。」 松田「合格した生徒の正答率だけでなく、受験に関するいろいろなデータが具体的な数値で見られるのは心強いですね。」 太田「ガゼットでは、受験情報を常にブラッシュアップして、受験生の皆さん、お父様・お母さまをサポートします。　ぜひ、ガゼットで志望校合格に向けて全力を尽くしましょう。」